Дистанційне навчання. Геометрія 7 клас. Вчитель Козлюк Є.Є.

Пояснення матеріалу 

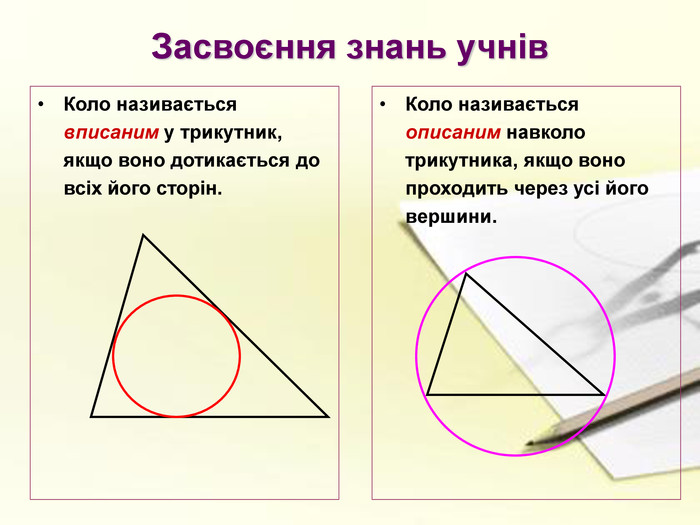
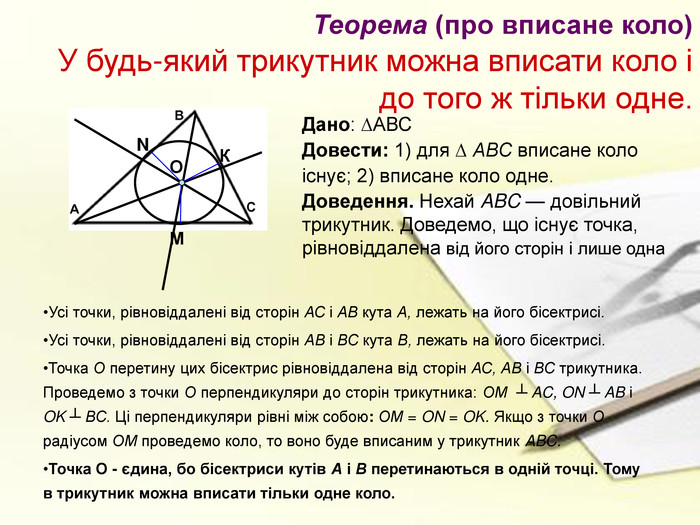
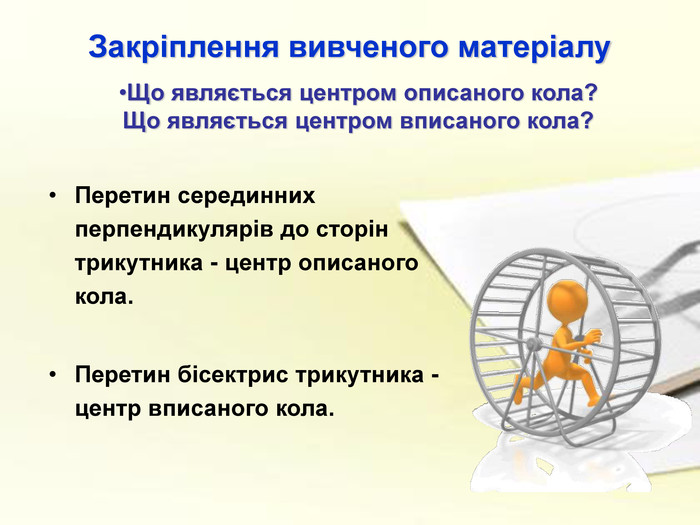
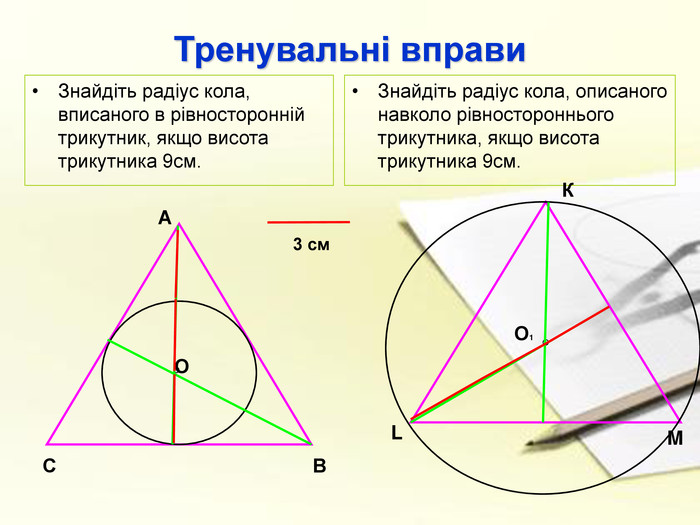
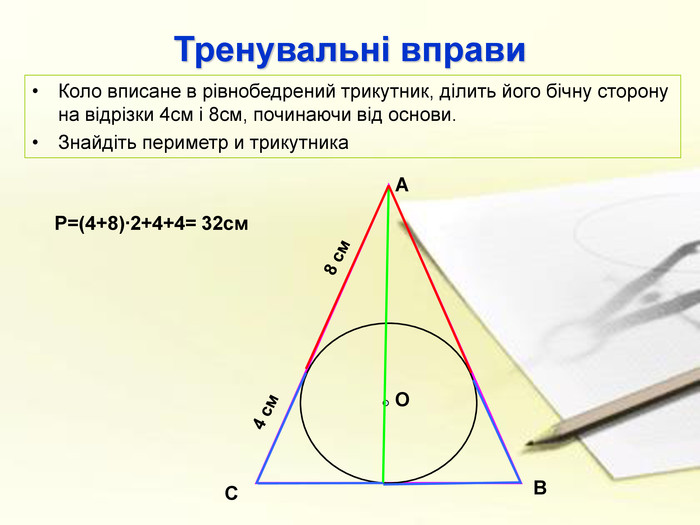
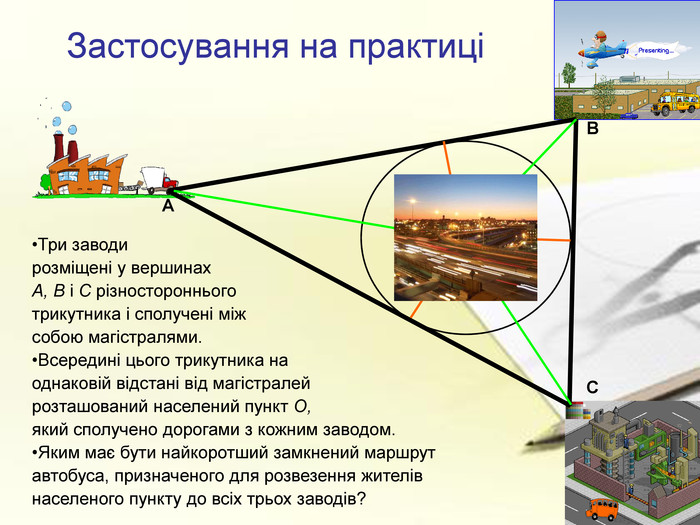
а також у підручнику парагрф 21 ст.166

Додаткове завдання

1. У рівнобедрений трикутник ABC (AB = BC) вписане коло з центром O

                                                     а) Доведіть, що трикутник AOC рівнобедрений. б) Знайдіть кут ABC, якщо  кут АОС                                                          100градусів. 

Виконати №550; №554; №557; №559; № 560 (підручник ст.171-172)

Підсумок уроку. Виконання усних вправ

1. Дано трикутник і коло. Визначте, чи є дане коло описаним навколо трикутника або вписаним у нього, якщо:

а) центр кола рівновіддалений від усіх сторін трикутника;

б) центр кола рівновіддалений від усіх вершин трикутника;

в) усі сторони трикутника — хорди кола;

г) усі сторони трикутника дотикаються до кола.

2. Точка O — центр кола, вписаного в трикутник ABC. Чи означає це, що:

а) OA = OB;

б)  точка O може лежати поза даним трикутником?

3. Навколо трикутника описано коло, і в нього вписано коло. Чи можуть ці кола мати рівні радіуси; спільний центр?