Дистанційне навчання. Алгебра 9 клас. Вчитель Дякова І.В.
Повторення
Урок №63
Тема: Функції. Властивості та графіки функцій y=kx+b, y=k/x, y=x2, y=√x, y=ax2+bx+c (a≠0)
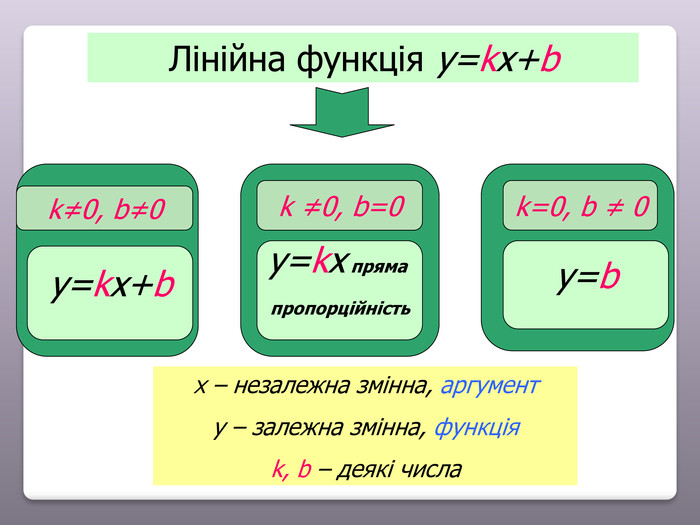
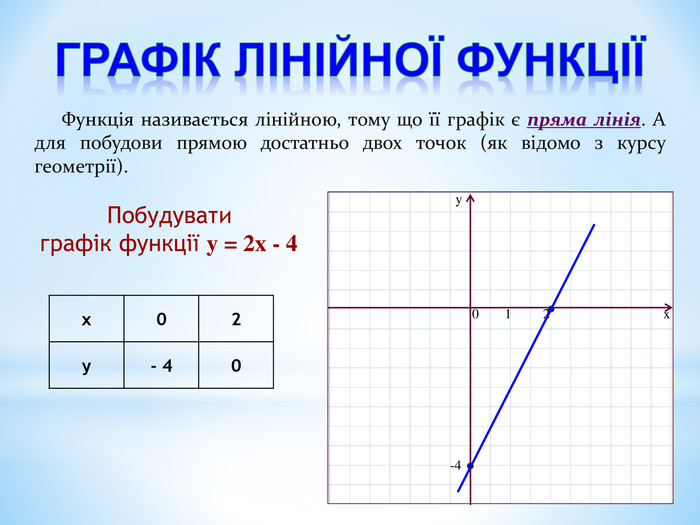
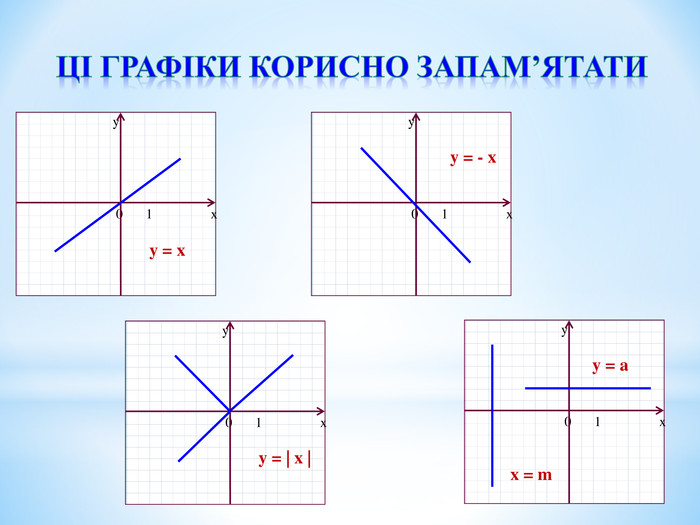
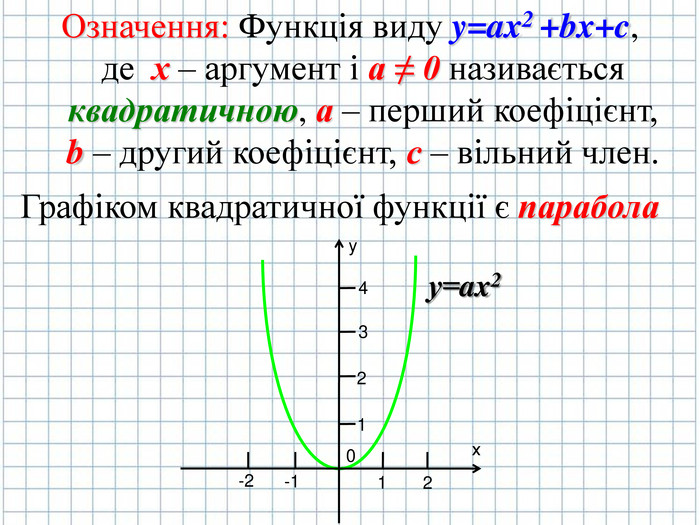

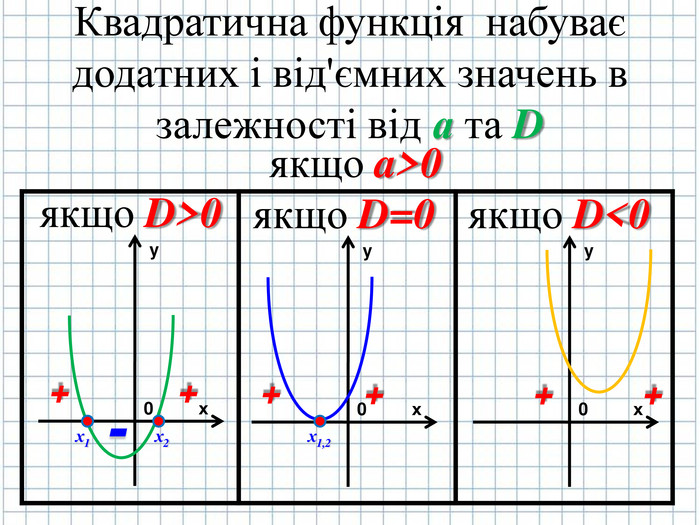
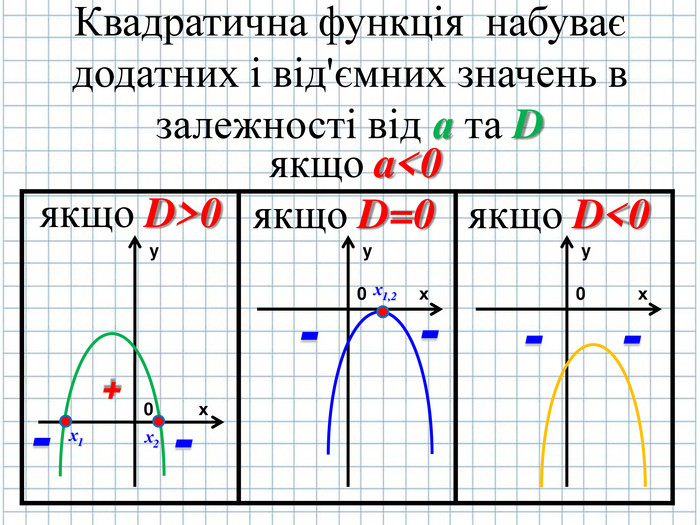
Побудуйте графік функції за таким планом

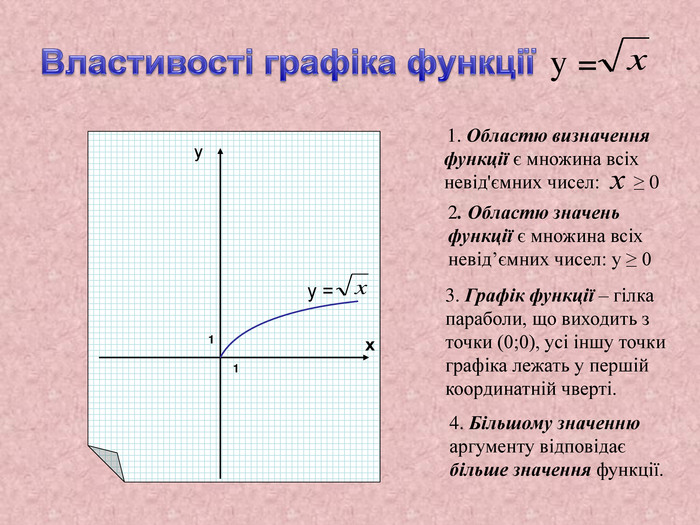
Тестові завдання
Дано функцію f (x) = x2 − 3х + 2.
Знайдіть f (−1)
1)6; 2)-2; 3)4; 4)2
Запитання 2
Знайдіть значення аргументу, при якому значення функції у = 3х + 2 дорівнює 8.
1)26; 2)2; 3)-2; 4)-26
Запитання 3

Знайдіть область визначення функції
1)D (y) = (–∞; 0)∪(0; 3)∪(3; +∞)
2) D (y) = (–∞; +∞)
3) D (y) = (–∞;3)∪(3; +∞)
4) D (y) = (–∞; 0)∪(0; +∞)
Запитання 4
Знайдіть область значень функції у = х2 − 4х + 1;
1)[-3;∾); 2)[3;∾); 3)[4;∾); 4)[-1;∾)
Запитання 5

Користуючись графіком функції, зображеної на рисунку, укажіть проміжки спадання функції.
1)[−3; −2]∪[1; 2]; 2)[−3; −2,5]∪[1,5; 2]; 3)(−3; −2)∪(1; 2]); 4)[−3; −1]∪[1; 2]
Запитання 6
Знайти нулі функції функції у = 3х + 2.
1)0; 2)-2/3; 3)-1,5; 4)-2
Запитання 7
В якій точці графік функції у = x2 − 3x + 2 перетинає вісь Oу?
1)(0;2); 2)(2;0); 3)(0;-2); 4)(-2;0)
Запитання 8

Графік якої функції зображено на рисунку ?
1)y=x2−2; 2)у=x2+2; 3) y=−x2−2; 4) y=−x2+2
Запитання 9

На рисунку зображено графік функції y= f(x) . Визначте проміжки зростання функції.
1)(-∞; 4] і [0;+∞); 2)[-6; -3] і [2;+∞); 3)[-3;2]; 4)визначити не можна
Запитання 10
Дано функцію у = 4х + 12. На якому проміжку функція набуває додатніх значень?
1)(3; +∞); 2)-3; +∞); 3)(-∞; -3); 4)[-3; +∞)
Запитання 11
В результаті паралельного перенесення графіка функції у = х² вздовж осі абсцис на 5 одиниць вправо отримали графік функції
1)у = (х+5)²; 2)у = х² + 5; 3)у = х² – 5; 4)у = (х – 5)²
Запитання 12
Графік функції у = х² зсунули ліворуч на 4 одиниці і підняли вгору на 6 одиниць . Графік якої функції отримали?
1)у = (х +4)² + 6; 2)у = (х – 4)² + 6; 3)у = (х +6)² + 4; 4)у = (х – 6)² - 4
Запитання 13
Знайти нулі функції у = 2х² - х + 12
1)3; 4.; 2)функція не має нулів; 3)-3;4; 4)3;-4
Запитання 14
у = 3х² - 6х. При яких значеннях аргументу функція набуває від′ємних значень?
1)[0;2]; 2)(0;2); 3)(0;2]; 4)[̄0;2)






