Дистанційне навчання. Геометрія 10 клас. Вчитель Дякова І.В.
Урок №43
Тема: Аксіоми стереометрії та наслідки з них. Паралельність прямих і площин (повторення)
Пригадуємо вивчений матеріал

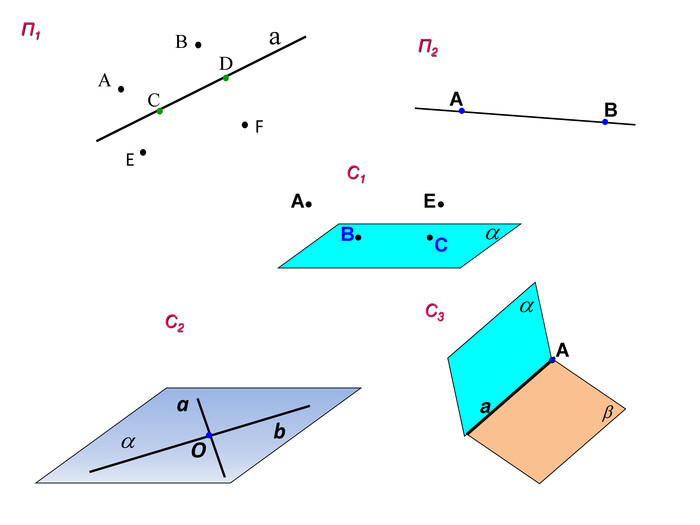

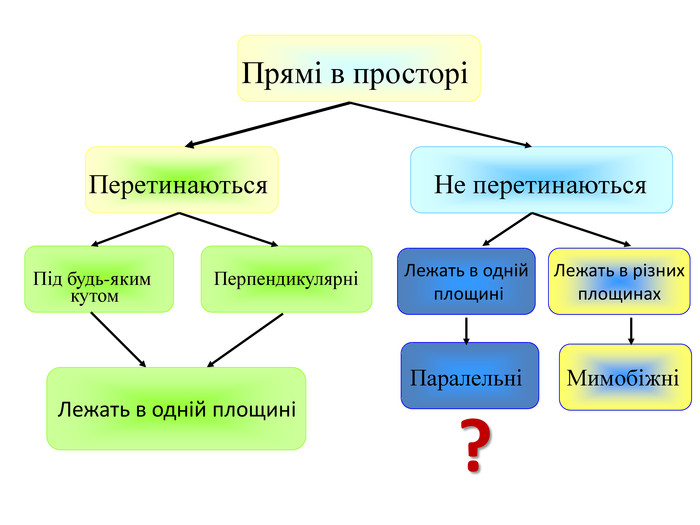
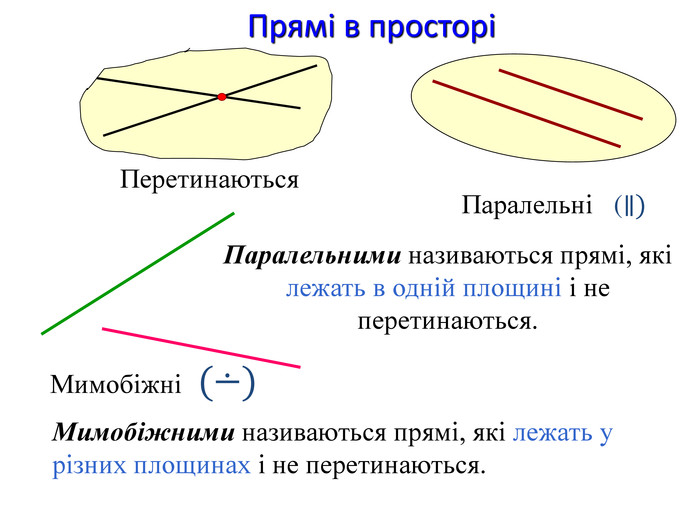
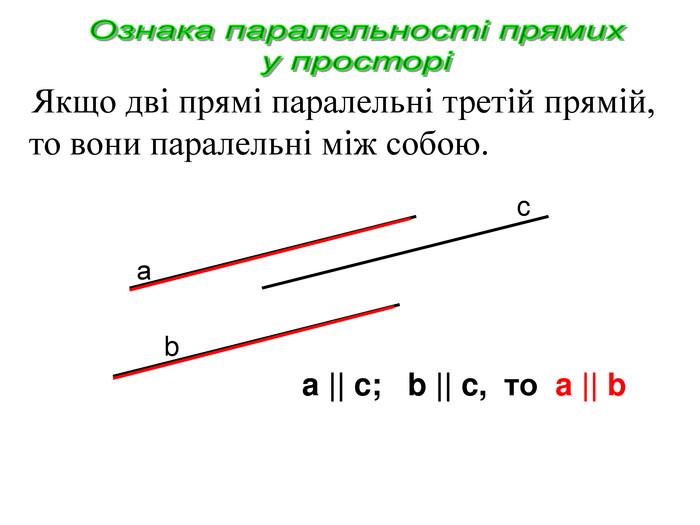

Виконайте тестові завдання
1) Геометрія - це наука, яка вивчає:
1) геометричні фігури у просторі;
2)геометричні фігури на площині;
3)властивості геометричних фігур;
4)просторові форми, відносини і їхні узагальнення.
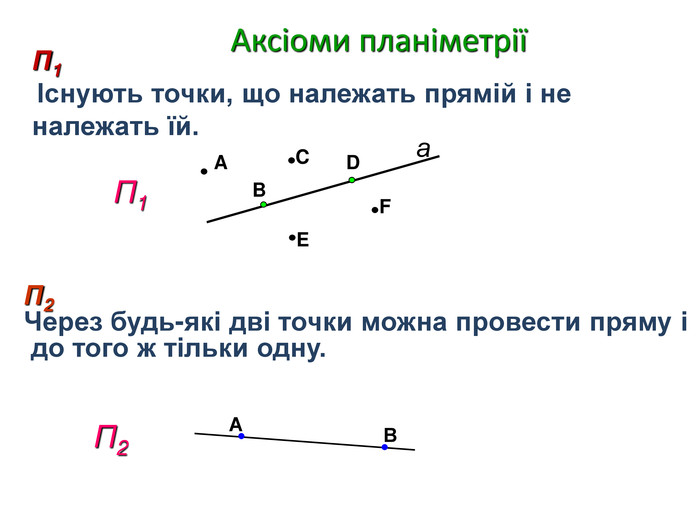
2) Яке з наведених тверджень є аксіомою планіметрії ?
1) Сума сумiжних кутiв дорiвнює 180°;
2)Яка б не була пряма, iснують точки, що належать цiй прямiй, i точки, що не належать їй;
3)Двi прямi на площинi називаються паралельними, якщо вони не перетинаються;
3) Яке з наведених тверджень є теоремою планіметрії?
2)Через будь-якi двi точки можна провести пряму i тiльки одну;
3)Кожний вiдрiзок має певну довжину, бiльшу вiд нуля;
4)Трикутник називається рівнобедреним, якщо двi його сторони рiвнi.
4) Яке з наведених тверджень правильне?
1) Через три точки завжди можна провести пряму i тiльки одну;
2)Через три точки в жодному разi не можна провести прямої;
3)Через одну точку можна провести 1 000 000 прямих;
4)Через будь-якi двi точки можна провести пряму i до того ж тільки одну.
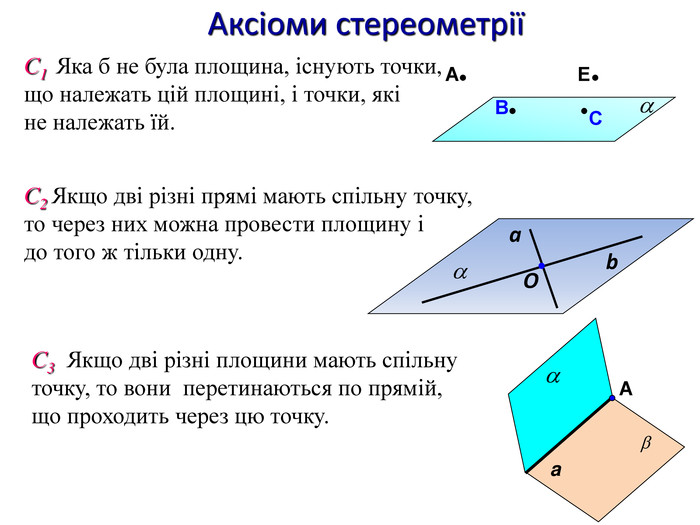
5) Яка з наведених фiгур не є основною фiгурою стереометрiї?
1) точка; 2) куля; 3) пряма; 4) площина.
6) Якщо дві різні площини мають точку,то вони:
1) мають безліч спільних точок, що утворюють пряму;
3)перетинаються по прямій, що проходить через цю точку;
4)утворюють кут з вершиною у цій точці.
7) Якщо дві точки прямої належать площині, то:
1) пряма й площина перетинаються;
2)і вся пряма належить цій площині;
4)пряма й площина перетинаються.
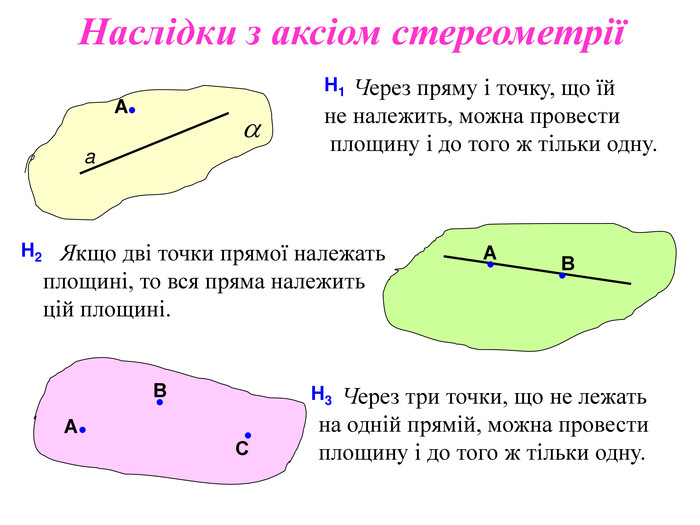
8) Через три точки, які не належать на одній прямій, можна провести:
9) Яке з наведених тверджень правильне?
1) Через три точки завжди можна провести пряму i тiльки одну;
2)Через три точки в жодному разi не можна провести прямої;
3)Через одну точку можна провести 1 000 000 прямих;
4)Через будь-якi двi точки можна провести пряму i до того ж тільки одну.
10) Через пряму й точку, яка не лежить на ній, можна провести:
